728x90
반응형
백준 1753 - 최단경로
* 자바로 구현
* 방향그래프가 주어지고 주어진 시작점에서 다른 모든 정점으로의
* 최단경로를 구하는 문제.
* 모든 가중치는 10이하.
* V <= 20000, E <= 300000
* 인접 행렬을 이용해서 그래프를 구성하면, 시간초과가 나온다.
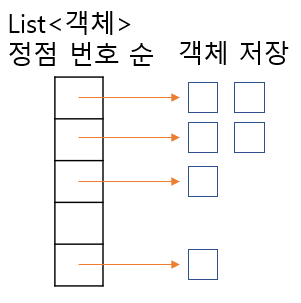
* 그렇기 때문에, 인접 리스트를 이용해서 구현해야한다.
* 시간을 더 줄이고자 한다면 , PriorityQueue와 함께 사용하면 된다고 한다.
* 여기서는 인접 리스트를 이용한 다익스트라 이용.
class Vertex_Link { // 정점 정보 저장.
int to, weight; // 이어진 다음 정점, 가중치
public Vertex_Link(int to, int weight) {
this.to = to;
this.weight = weight;
}
}
public class BOJ_1753_Min_Path {
private static int V, E, distance[]; // 정점수, 간선수, 정점과의 거리
private final static int INFINITY = Integer.MAX_VALUE;
private static List<Vertex_Link>[] vlist;
private static boolean visited[];
public static void main(String[] args) throws Exception {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer stt = new StringTokenizer(br.readLine());
V = Integer.parseInt(stt.nextToken());
E = Integer.parseInt(stt.nextToken());
distance = new int[V+1];
vlist = new ArrayList[V+1]; // 객체 리스트를 정점수 만큼 초기화
visited = new boolean[V+1];
Arrays.fill(distance, INFINITY); // distance 배열을 무한대로 채움.
int start_Vertex = Integer.parseInt(br.readLine());
for( int i = 1; i <= V; i++) {
vlist[i] = new ArrayList<>(); // 각 정점마다 초기화
}
for( int i = 1; i <= E; i++) {
stt = new StringTokenizer(br.readLine());
int v = Integer.parseInt(stt.nextToken());
int to = Integer.parseInt(stt.nextToken());
int w = Integer.parseInt(stt.nextToken());
vlist[v].add(new Vertex_Link(to, w)); // 해당 정점 번호의 리스트에 정보 저장.
}
dijkstra(start_Vertex); // 다익스트라 실행
for(int i = 1; i <= V; i++) {
if(distance[i] == INFINITY) { // 갈 수 없는 경우
System.out.println("INF");
continue;
}
System.out.println(distance[i]);
}
}
/** 다익스트라 경로 찾기 */
private static void dijkstra(int start_Vertex) {
int min = 0, current = 0; // 최소값, 현재위치.
distance[start_Vertex] = 0; // 처음 자기 자신의 정점은 거리 0
for( int i = 1; i <= V; i++) {
min = INFINITY;
for( int j = 1; j <= V; j++) {
// 방문 한 적이 없고, 거리 값보다 최소 값이 크다면
if(!visited[j] && min > distance[j]) {
min = distance[j]; // 최소 값 갱신.
current = j; // 위치 저장.
}
}
visited[current] = true; // 위치 방문
if(vlist[current].isEmpty()) continue; // 이어진 정점이 없다면 다음 정점으로
for(Vertex_Link v : vlist[current]) { // 현재 정점에 이어진 모든 정점 비교
// 방문한 적이 없고, 최소값에 가중치를 더한 값이 더 작다면?
if(!visited[v.to] && distance[v.to] > min+v.weight) {
distance[v.to] = min + v.weight; // 거리 갱신.
}
}
}
}
}반응형
'문제풀이 > 백준 문제풀이' 카테고리의 다른 글
| [ 알고리즘 ] 코딩 백준 17471 - 게리맨더링.java (0) | 2020.09.07 |
|---|---|
| [ 알고리즘 ] 코딩 백준 17144 - 미세먼지 안녕!!.java (0) | 2020.09.07 |
| [ 알고리즘 ] 코딩 백준 2933 - 미네랄.java (0) | 2020.09.07 |
| [ 알고리즘 ] 코딩 백준 15961 - 회전초밥.java (0) | 2020.09.07 |
| [ 알고리즘 ]코딩 백준 9663 - N-Queen - 1차원배열을 이용해서 구현.java (0) | 2020.09.05 |



